Quantum field theory

Quantum Field Theory (QFT) is the fundamental tool to describe the behaviour of elementary particles and fundamental interactions. Currently, we have a strong grasp of QFT at perturbative level, while a full understanding of non-perturbative aspects remains an active area of research. The main research directions include:

Geometry and topology: non-linear sigma models; Batalin–Vilkovisky quantisation in the Alexandrov–Kontsevich–Schwartz–Zaboronsky geometric formulation; higher gauge theory.

Worldline methods: methods in first quantization, inspired by string theory, to study scattering amplitudes and effective actions in gauge and gravitational theories.

Anomalies: properties and physical implications of chiral and trace quantum anomalies.

Renormalization group: study of QFT using both perturbative and non-perturbative methods in arbitrary dimensions; functional renormalisation group, either perturbative or Wilsonian, to determine universal properties, symmetries, and renormalisability of scale-invariant or conformal theories; effective actions and S-matrix. 

Integrability: exact computation of physical quantities via quantum integrability with applications in non-equilibrium physics, entanglement, spin chains, renormalisation group in 2D QFT, as well as in 4D N=2 supersymmetric gauge theories for phenomenological implications and in correspondence with perturbations of gravitational solutions, black holes and gravitational waves.

Research activities

Topological and geometrical aspects of quantum field theory and strings:

Non-linear sigma models. Batalin-Vilkovisky quantisation using the geometrical formulation of Alexandrov-Kontsevich-Schwartz-Zaboronsky. Higher gauge theories.

Worldline methods

Study of first quantisation techniques, known as “worldline methods”. The goal is to find  new representations of scattering amplitudes and effective actions in QFT with gauge and gravitational couplings, with string inspired methods .

Anomalies in QFT

Anomalies describe the quantum breaking of classical symmetries. They have several applications which range from constraining the matter content of gauge theories to the  characterisation of non-perturbative properties of QFT and their behaviour under the action of the renormalisation group .

QFT, CFT in d>2 and renormalisation group

The abstract space of all possible quantum field theories is characterised by points which are invariant under scale or conformal transformations (renormalisation group fixed points). Considering the symmetries determined by the spin content, we formulate new UV complete quantum field theories and study new classes of universality in statistical theories and in the construction of new models for fundamental interactions beyond the Standard Model.

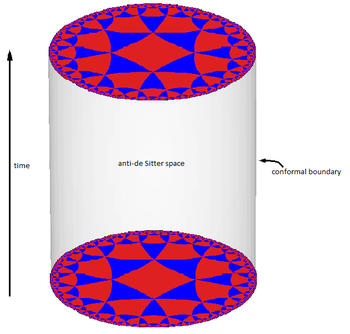
Integrability:  supersymmetry in 4D, strings and Bethe ansatz

Integrability is a fundamental property of a class of theories that allows to calculate exactly non-trivial physical properties of a given system, thanks to an underlying mathematical and physical structure. In general, this property becomes manifest in a natural way in 2D systems. In higher dimensions, it becomes then even more remarkable. Our interest is towards supersymmetric gauge theories in 4D, which also feature phenomenological applications, and their relationship with string theories, where the bidimensional structure automatically leads to integrability. Our final goal is to formulate models that are more fundamental and therefore can provide realistic description of the interactions. In integrable quantum field theories it is possible to consider, in an exact and unified way, the problems of thermodynamic behaviour and finite volume effects, using the Thermodynamic Bethe Ansatz (TBA). The development of the mathematical structures underlying TBA has revealed surprising algebraic and analytical textures, connected to other lines of research in mathematics and physics, which are under active investigation nowadays.

Non-equilibrium physics and quantum fields

Non-equilibrium physics is one of the major challenges of modern statistical mechanics. Recent developments have highlighted the existence of QFT methods to study these phenomena, not just at classical, but also at quantum level where they are related to the physics of cold atoms and bosonic condensates. The “quantum quench” approach is now mature, while generalised hydro-dynamics (GHD) is in an active phase of recent development. Integrability and non-perturbative physics play a crucial role in both approaches.

String compactifications

Study of the supergravity effective field theory in four dimensions for string compactifications on Calabi-Yau manifolds with branes, orientifolds and background fluxes. Derivation of perturbative and non-perturbative corrections. Stabilisation of both closed and open string moduli. Mechanisms to break supersymmetry and to realise de Sitter vacua in chiral D-brane models which are globally consistent and give rise to promising applications to cosmology and particle physics.

QFT in curved spaces

Development of quantum field theory methods in curved spaces, mainly renormalisation group techniques, for applications to problems in quantum gravity and cosmology.

National and international projects and collaborations

Our research activities are also supported by the INFN initiatives ST&FI, GAST, FLAG. Several collaborations with national (Modena, Trieste, Roma, Padova) and foreign [Morelia (MX), Potsdam (DE), Cambridge (UK), Oxford (UK), Durham (UK), King’s College (UK), City University (UK), DESY (DE), Heidelberg (DE), Perimeter (CA), Texas A&M (US), Colorado (US), Oklahoma (US), New Mexico (US), HRI Institute (IN), Ewha Seoul (KR), ENS Paris (FR), Saclay (FR), Melbourne (AU), BME Budapest (HU) ]  institutions are active.